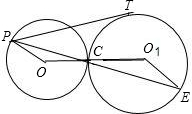
 证明:如图所示,⊙O1,⊙O,两圆半径分别为R、r. 延长PC与圆交于E点,连接O1E,PO,OO1, ∵OP=OC,O1C=O1E, ∴∠OCP=∠OPC,∠O1CE=∠O1EC. 又∵∠OCP与∠O1CE是对顶角, ∴∠OCP=∠O1CE, ∴∠OCP=∠OPC=∠O1CE=∠O1EC, ∴△OCP∽△O1CE, ∴
∵PT与⊙O1相切于点T, ∴PT2=PC?PE=PC?(PC+CE)=PC?(PC+
即PT2=PC2(1+
∴PC:PT=
|
 证明:如图所示,⊙O1,⊙O,两圆半径分别为R、r. 延长PC与圆交于E点,连接O1E,PO,OO1, ∵OP=OC,O1C=O1E, ∴∠OCP=∠OPC,∠O1CE=∠O1EC. 又∵∠OCP与∠O1CE是对顶角, ∴∠OCP=∠O1CE, ∴∠OCP=∠OPC=∠O1CE=∠O1EC, ∴△OCP∽△O1CE, ∴
∵PT与⊙O1相切于点T, ∴PT2=PC?PE=PC?(PC+CE)=PC?(PC+
即PT2=PC2(1+
∴PC:PT=
|
题目简介
已知:⊙O与⊙O1外切于C,P是⊙O上任一点,PT与⊙O1相切于点T.求证:PC:PT是定值.-数学
题目详情