 (1)∵M是AB的中点, ∴OC⊥AB, ∵OM=MC, ∴BC=OB, ∴OB=OC=BC, ∴△OBC是等边三角形, ∴∠OCB=60°; (2)证明:连接OA, ∵∠AOC=2∠ABC,∠BAD=2∠ABD, ∴∠AOC=∠BAD, ∵∠AOC+∠OAB=90°, ∴∠OAD=∠AOB+∠BAD=∠OAB+∠AOC=90°, 即OA⊥AD, ∴AD是⊙O的切线. |
 (1)∵M是AB的中点, ∴OC⊥AB, ∵OM=MC, ∴BC=OB, ∴OB=OC=BC, ∴△OBC是等边三角形, ∴∠OCB=60°; (2)证明:连接OA, ∵∠AOC=2∠ABC,∠BAD=2∠ABD, ∴∠AOC=∠BAD, ∵∠AOC+∠OAB=90°, ∴∠OAD=∠AOB+∠BAD=∠OAB+∠AOC=90°, 即OA⊥AD, ∴AD是⊙O的切线. |
题目简介
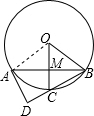
如图,在⊙O中,AB是弦,半径OC经过AB的中点M,(1)若OM=MC,求∠OCB的度数;(2)作∠BAD=2∠ABD,AD交BC的延长线于D,求证:AD是⊙O的切线.-数学
题目详情
(1)若OM=MC,求∠OCB的度数;
(2)作∠BAD=2∠ABD,AD交BC的延长线于D,求证:AD是⊙O的切线.