首页 > 如图，Rt△ABC中，∠C=90°、∠A=30°，在AC边上取点O画圆，使⊙O经过A、B两点，下列结论正确的序号是______（多填或错填得0分，少填酌情给分）．①AO=2CO；②AO=BC；③以O为

如图，Rt△ABC中，∠C=90°、∠A=30°，在AC边上取点O画圆，使⊙O经过A、B两点，下列结论正确的序号是______（多填或错填得0分，少填酌情给分）．①AO=2CO；②AO=BC；③以O为

题目简介

如图，Rt△ABC中，∠C=90°、∠A=30°，在AC边上取点O画圆，使⊙O经过A、B两点，下列结论正确的序号是______（多填或错填得0分，少填酌情给分）．①AO=2CO；②AO=BC；③以O为

题目详情

如图，Rt△ABC中，∠C=90°、∠A=30°，在AC边上取点O画圆，使⊙O经过A、B两点，下列结论正确的序号是______（多填或错填得0分，少填酌情给分）．
①AO=2CO；②AO=BC；③以O为圆心，以OC为半径的圆与AB相切；④延长BC交⊙O与D，则A、B、D是⊙O的三等分点．
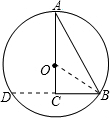
360优课网
题型：填空题难度：中档来源：沁阳市一模

答案


360优课网
连接OB，∴OA=OB，
∴∠A=∠ABO，
∵∠C=90°，∠A=30°，
∴∠ABC=60°，
∴∠OBC=30°，
∴OC=class="stub"1
2
OB=class="stub"1
2
OA，
即OA=2OC，
故①正确；
∵cos∠OBC=class="stub"BC
OB
，
∴BC=
3
2
OB，
即BC=
3
2
OA，
故②错误；
∵∠ABO=∠OBC=30°，
∴点O在∠ABC的角平分线上，
∴点O到直线AB的距离等于OC的长，
即以O为圆心，以OC为半径的圆与AB相切；
故③正确；
延长BC交⊙O于D，
∵AC⊥BD，
∴AD=AB，
∴△ABD为等边三角形，
∴






AD
=






AB
=






BD
，
∴点A、B、D将⊙O的三等分．
故④正确．
故答案为①③④．

更多内容推荐

Copyright © 2018-2020 360优课网