| (1)∵AD=1,∠DAE=90°, ∴
同理,
所以,点D运动到点G所经过的路线长l=l1+l2+l3=3π. 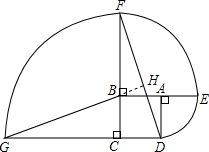 (2)直线GB⊥DF. 理由如下:延长GB交DF于H. ∵CD=CB,∠DCF=∠BCG,CF=CG, ∴△FDC≌△GBC. ∴∠F=∠G, 又∵∠F+∠FDC=90°, ∴∠G+∠FDC=90°, 即∠GHD=90°, 故GB⊥DF. |
| (1)∵AD=1,∠DAE=90°, ∴
同理,
所以,点D运动到点G所经过的路线长l=l1+l2+l3=3π.  (2)直线GB⊥DF. 理由如下:延长GB交DF于H. ∵CD=CB,∠DCF=∠BCG,CF=CG, ∴△FDC≌△GBC. ∴∠F=∠G, 又∵∠F+∠FDC=90°, ∴∠G+∠FDC=90°, 即∠GHD=90°, 故GB⊥DF. |
题目简介
如图,ABCD是边长为1的正方形,其中DE、EF、FG的圆心依次是A、B、C.(1)求点D沿三条圆弧运动到点G所经过的路线长;(2)判断直线GB与DF的位置关系,并说明理由.-数学
题目详情
(1)求点D沿三条圆弧运动到点G所经过的路线长;
(2)判断直线GB与DF的位置关系,并说明理由.