 (1)连接BC, ∵C是
∴∠CAD=∠ABC, 又∵AB是直径, ∴∠ACB=90°,又CF⊥AB, ∴∠ACF=∠ABC, ∴∠CAD=∠ACF, ∴△AEC是等腰三角形; (2)连接BD, 在Rt△ABD中,∠DAB=30°,AB=4,则BD=2, 设∠CAD=∠ACF=x, ∴∠DAB+2x=90°, ∴2x=60°,即∠CAB=60°,∴CBA=30°, ∴AC=
,∴AC=BD=2, 在△ACF中,AF=
∴AE=
∴CE=
|
 (1)连接BC, ∵C是
∴∠CAD=∠ABC, 又∵AB是直径, ∴∠ACB=90°,又CF⊥AB, ∴∠ACF=∠ABC, ∴∠CAD=∠ACF, ∴△AEC是等腰三角形; (2)连接BD, 在Rt△ABD中,∠DAB=30°,AB=4,则BD=2, 设∠CAD=∠ACF=x, ∴∠DAB+2x=90°, ∴2x=60°,即∠CAB=60°,∴CBA=30°, ∴AC=
,∴AC=BD=2, 在△ACF中,AF=
∴AE=
∴CE=
|
题目简介
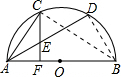
如图,C是AD的中点,CF⊥AB,F为垂足.(1)求证:△AEC是等腰三角形.(2)设AB=4,∠DAB=30°,求CE的长.-数学
题目详情
(1)求证:△AEC是等腰三角形.
(2)设AB=4,∠DAB=30°,求CE的长.