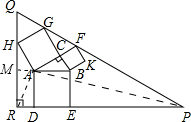
 延长BA交QR于点M,连接AR,AP. ∵AC=GC,BC=FC,∠ACB=∠GCF, ∴△ABC≌△GFC, ∴∠CGF=∠BAC=30°, ∴∠HGQ=60°, ∵∠HAC=∠BAD=90°, ∴∠BAC+∠DAH=180°, 又∵AD∥QR, ∴∠RHA+∠DAH=180°, ∴∠RHA=∠BAC=30°, ∴∠QHG=60°, ∴∠Q=∠QHG=∠QGH=60°, ∴△QHG是等边三角形. AC=AB?cos30°=8×
则QH=HA=HG=AC=4
在直角△HMA中,HM=AH?sin60°=4
在直角△AMR中,MR=AD=AB=8. ∴QR=QH+HM+MR=4
∴QP=2QR=28+8
PR=QR?
∴△PQR的周长等于RP+QP+QR=54+26
故答案为:54+26
|
题目简介
勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在-数学
题目详情