如图：在△ABC中，∠C=90°，AC=BC，D是斜边AB的中点，点E、F分别是边AC、BC上两个动点，且ED⊥DF．（1）当E、F分别在AC、BC边上移动时，并保持∠EDF=90°，DE、DF是否相

题目简介

题目详情

如图：在△ABC中，∠C=90°，AC=BC，D是斜边AB的中点，点E、F分别是边AC、BC上两个动点，且ED⊥DF．
（1）当E、F分别在AC、BC边上移动时，并保持∠EDF=90°，DE、DF是否相等？请证明你的结论．
（2）当E、F分别在AC、BC上移动时，并保持∠EDF=90°，S_{四边形DECF}会随着变化吗？请证明你的结论．
（3）S_{四边形DECF}=5cm²时，求AC的长． 360优课网

题型：解答题难度：中档来源：不详

答案

（1）DE=DF．
理由如下：如图，连接CD，
∵AC=BC，D是AB的中点，
∴CD是∠ACB的平分线，
作DM⊥AC，DN⊥BC，垂足分别为点M、N，
则∠DME=∠DNF=90°，DM=DN（角平分线上的点到角的两边距离相等），
又∵∠C=90°，
∴四边形CMDN是正方形，
∴∠MDN=90°，
∴∠MDF+∠FDN=90°，
∵∠EDF=90°，
∴∠EDM+∠MDF=90°，
∴∠EDM=∠FDN，
在△DEM和△DFN中，
∵

∠DME=∠DNF=90°

DM=DN

∠EDM=∠FDN

，
∴△DEM≌△DFN（ASA），
∴DE=DF；

（2）S四边形DECF不会变化．
理由如下：根据（1）可得△DEM≌△DFN，
所以S△DEM=S△DFN，
所以S四边形DECF=S正方形CMDN，
∵点D是斜边AB边的中点，
∴CD=class="stub"1

AB（不变），
∴正方形CMDN的面积不变，
∴S四边形DECF不会变化；

（3）∵S四边形DECF=5cm2，
∴class="stub"1

CD2=5（正方形的面积等于对角线乘积的一半），
解得CD=

，
AC=

CD=

（等腰直角三角形斜边等于直角边的

倍）．

上一篇 : 母婴传播是艾滋病的传播途径之
下一篇 : 已知：在四边形ABCD中，BC＞BA，∠A+∠

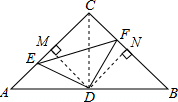
如图：在△ABC中，∠C=90°，AC=BC，D是斜边AB的中点，点E、F分别是边AC、BC上两个动点，且ED⊥DF．（1）当E、F分别在AC、BC边上移动时，并保持∠EDF=90°，DE、DF是否相

题目简介

题目详情

答案

更多内容推荐