| (1)能.(2分) 由题意,∠B+∠ACB=∠E+∠DFE,∠B≠∠E、∠B≠∠DFE,(4分) 设∠B<∠DFE, 作∠EFG=∠B,G在DE上,(5分) 作∠BCH=∠E,H在AB上(如图),(6分) 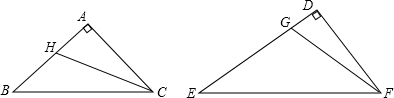 可得,△HBC∽△GFE; ∵∠AHC=∠B+∠BCH,∠DGF=∠E+∠EFG, ∴∠AHC=∠DGF, 又∠A=∠D, ∴△AHC∽△DGF.(8分) (2)不唯一,作∠CBM=∠F,∠FEN=∠C即可. 此时△BCM∽△FEN,△ABM∽△DEN. |
| (1)能.(2分) 由题意,∠B+∠ACB=∠E+∠DFE,∠B≠∠E、∠B≠∠DFE,(4分) 设∠B<∠DFE, 作∠EFG=∠B,G在DE上,(5分) 作∠BCH=∠E,H在AB上(如图),(6分)  可得,△HBC∽△GFE; ∵∠AHC=∠B+∠BCH,∠DGF=∠E+∠EFG, ∴∠AHC=∠DGF, 又∠A=∠D, ∴△AHC∽△DGF.(8分) (2)不唯一,作∠CBM=∠F,∠FEN=∠C即可. 此时△BCM∽△FEN,△ABM∽△DEN. |
题目简介
如图,已知△ABC和△DEF,∠A=∠D=90°,且△ABC与△DEF不相似,问是否存在某种直线分割,使△ABC所分割成的两个三角形与△DEF所分割成的两个三角形分别对应相似?(1)如果存在,请你设-
题目详情
(1)如果存在,请你设计出分割方案,并给出证明;如果不存在,请简要说明理由;
(2)这样的分割是唯一的吗?若还有,请再设计出一种.