 证明:连接AC和BD. ∵弦CD垂直于直径AB, ∴BC=BD.(5分) ∴∠BCD=∠BDC. ∵OA=OC, ∴∠OCA=∠OAC. ∵∠BDC=∠OAC, ∴∠BCD=∠OCA. ∴△BCD∽△OCA. ∴
在△CDN和△CAM中, ∵∠DCN=∠ACM,∠CDN=∠CAM, ∴△CDN∽△CAM.(20分) ∵
∴CN=
|
 证明:连接AC和BD. ∵弦CD垂直于直径AB, ∴BC=BD.(5分) ∴∠BCD=∠BDC. ∵OA=OC, ∴∠OCA=∠OAC. ∵∠BDC=∠OAC, ∴∠BCD=∠OCA. ∴△BCD∽△OCA. ∴
在△CDN和△CAM中, ∵∠DCN=∠ACM,∠CDN=∠CAM, ∴△CDN∽△CAM.(20分) ∵
∴CN=
|
题目简介
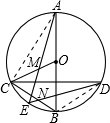
如图,在⊙O中,弦CD垂直于直径AB.M是OC的中点,AM的延长线交⊙O于E,DE交BC于N.求证:BN=CN.-数学
题目详情