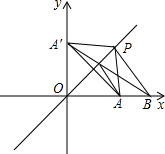
 如图,作A关于直线y=x的对称点A′, 则PA=PA′, 故PA+PB=PA′+PB, 由图知,只有当A、P、B共线时,PA+PB最小, 又由A与A′关于y=x对称知,A′(0,2), 由A′、B两点坐标得A′B直线方程:
联立
解得 x=y=
故当PA+PB最小时,P的坐标为:(
故答案为:(
|
 如图,作A关于直线y=x的对称点A′, 则PA=PA′, 故PA+PB=PA′+PB, 由图知,只有当A、P、B共线时,PA+PB最小, 又由A与A′关于y=x对称知,A′(0,2), 由A′、B两点坐标得A′B直线方程:
联立
解得 x=y=
故当PA+PB最小时,P的坐标为:(
故答案为:(
|
题目简介
在平面直角坐标系中,A(2,0),B(3,0),P是直线y=x上的点,当PA+PB最小时,P点的坐标为______.-数学
题目详情