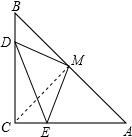
 甲乙两位同学的判断都正确. 如图,连接CM,∵M是等腰直角△ABC的中点, ∴BM=CM,∠ACM=∠B=45°,∠CMB=90°, ∵∠DME=90°, ∴∠BMD+∠CMD=90°, ∠CME+∠CMD=90°, ∴∠BMD=∠CME, 在△BMD和△CME中,
∴△BMD≌△CME(ASA), ∴MD=ME, ∴△MDE是等腰直角三角形, 因此,△MDE的形状不会发生变化,故甲的说法正确; S四边形MECD=S△CME+S△CME=S△BMD+S△CME=S△CBCM,不变,所以,乙的说法正确, 综上所述,甲乙两位同学的判断都正确. |
题目简介
如图(1),将一直角三角形的直角顶点M放在腰长为4的等腰直角三角形ABC斜边的中点,另两条直角边分别与线段BC,AC交于D,E两点,当绕着直角顶点M旋转时,该直角三角形两直角边-数学
题目详情