 证明:(1)∵AC=BC ∴∠CAB=∠CBA, 又∵E是内心, ∴∠1=∠2=∠3=∠4. ∴BE=AE; (2)∵∠BED=∠1+∠3,∠EDB=∠2+∠5, 又∵∠5=∠4, ∴∠BED=∠EDB, ∴BD=DE, ∴
又∵∠D=∠C ∴△ABC∽△EBD, ∴
∵BE=AE, ∴
|
 证明:(1)∵AC=BC ∴∠CAB=∠CBA, 又∵E是内心, ∴∠1=∠2=∠3=∠4. ∴BE=AE; (2)∵∠BED=∠1+∠3,∠EDB=∠2+∠5, 又∵∠5=∠4, ∴∠BED=∠EDB, ∴BD=DE, ∴
又∵∠D=∠C ∴△ABC∽△EBD, ∴
∵BE=AE, ∴
|
题目简介
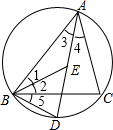
如图,在△ABC中,AC=BC,E是内心,AE的延长线交△ABC的外接圆于D.求证:(1)BE=AE;(2)ABAC=AEDE.-数学
题目详情
求证:(1)BE=AE;
(2)