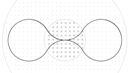
 (1)粒子离开出发点最远的距离为轨道半径的2倍 几何关系,则有R0=2r=
根据半径公式,解得v=
(2)磁场的大小变为
根据几何关系可以得到,当弦最长时,运动的时间最长,弦为2 R0时最长,圆心角60° 解得:t=
(3)根据矢量合成法则,叠加区域的磁场大小为
R0以为的区域磁场大小为
根据对称性画出情境图,由几何关系可得R1的最小值为(
T=
答:(1)求带电粒子的速率得v=
(2)若粒子源可置于磁场中任意位置,且磁场的磁感应强度大小变为
(3)若原磁场不变,再叠加另一个半径为R1(R1>R0)圆形匀强磁场,磁场的磁感应强度的大小为
|
题目简介
如图所示,空间存在一个半径为R0的圆形匀强磁场区域,磁场的方向垂直于纸面向里,磁感应强度的大小为B.有一个粒子源在纸面内沿各个方向以一定速率发射大量粒子,粒子的质量为-物理
题目详情
(1)求带电粒子的速率.
(2)若粒子源可置于磁场中任意位置,且磁场的磁感应强度大小变为
(3)若原磁场不变,再叠加另一个半径为R1(R1>R0)圆形匀强磁场,磁场的磁感应强度的大小为