如图，板长为l、间距为d的平行金属板水平放置，两板间所加电压大小为U，在极板的右侧相距为a处有与板垂直的足够大光屏PQ，一带正电的粒子以初速度v0从两板正中间平行两板射入-物理

题目简介

题目详情

如图，板长为l、间距为d的平行金属板水平放置，两板间所加电压大小为U，在极板的右侧相距为a处有与板垂直的足够大光屏PQ，一带正电的粒子以初速度v₀从两板正中间平行两板射入，从两板间射出时速度的偏转角为37°，不计粒子受到的重力．（cos37°=0.8，sin37°=0.6）

360优课网

（1）求粒子的比荷q/m；
（2）若在两板右侧MN和光屏PQ间加如图所示的磁场，要使粒子不打在光屏上，求磁感应强度B大小的取值范围；
（3）若在两板右侧MN和光屏PQ间加垂直纸面向外、大小为E₀的匀强电场，设初速度方向所在直线与光屏交点为O点，取O点为坐标原点，水平向右为x正方向，垂直纸面向外为z轴的正方向，建立如图所示的坐标系，求粒子打在光屏上的坐标（x，y，z）．

题型：问答题难度：中档来源：宿迁一模

答案

（1）由题意知，粒子在电场中偏转时做类平抛运动，设粒子从两版间射出时，速度的水平分量为vx，竖直分量为vy则由题意有：
vx=v0
vy=at=class="stub"qU

×class="stub"l

=class="stub"qUl

mdv0

又因为粒子从电场射出时速度的偏转角为37° 则有：tan370=

=class="stub"qUl

解之得：class="stub"q

4Ul

（2）由题意得，粒子进入磁场的速度vcos37°=v0得v=class="stub"5

v0
设粒子刚好打在光屏时，磁感应强度为B，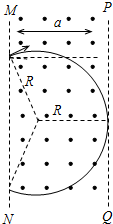

360优课网

如图，由几何知识有：Rsin37°+R=a 得：R=class="stub"a

1+sin37°

粒子在磁场中做圆周运动，洛伦兹力提供向心力有：Bqv=

mv2

得：B=class="stub"mv

=class="stub"1

class="stub"q

class="stub"5

class="stub"a

1+sin37°

=class="stub"8Ul

3dv0a

所以，要使粒子不大在光屏上，应有磁感应强度小于class="stub"8Ul

3dv0a

（3）由题知：
微粒只要打在屏上，x坐标就为0
微粒在y轴方向先做匀加速直线运动，后做匀速直线运动，根据几何关系可得：
y=(class="stub"l

+a)tan37°=class="stub"3l+6a

微粒在z轴方向在电场力作用下做初速度为0的匀加速直线运动，根据位移时间关系有：
z=class="stub"1

qE0

×t2
根据运动的等时性有在z轴方向运动时间t=class="stub"a

代入得：z=

3E0da2

8Ul

（1分）
则坐标为：（0，class="stub"3l+6a

，

3E0da2

8Ul

）
答：（1）粒子的比荷class="stub"q

4Ul

；
（2）若在两板右侧MN和光屏PQ间加如图所示的磁场，要使粒子不打在光屏上，磁感应强度小于class="stub"8Ul

3dv0a

；
（3）若在两板右侧MN和光屏PQ间加垂直纸面向外、大小为E0的匀强电场，设初速度方向所在直线与光屏交点为O点，取O点为坐标原点，水平向右为x正方向，垂直纸面向外为z轴的正方向，建立如图所示的坐标系，粒子打在光屏上的坐标：（0，class="stub"3l+6a

，

3E0da2

8Ul

）．

上一篇 : 如图，一束带正电粒子（不计重力）自
下一篇 : 如图所示，空间存在一个半径为R0

如图，板长为l、间距为d的平行金属板水平放置，两板间所加电压大小为U，在极板的右侧相距为a处有与板垂直的足够大光屏PQ，一带正电的粒子以初速度v0从两板正中间平行两板射入-物理

题目简介

题目详情

答案

更多内容推荐