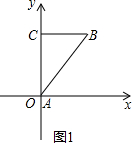
 (1)当点A在原点时,如图1,AC在y轴上,BC⊥y轴, 所以点B的坐标是(2,2). (2)当OA=OC时,如图2, 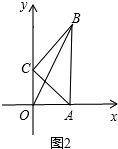 △OAC是等腰直角三角形,AC=2, 所以∠OAC=∠OCA=45°,OA=OC=
∵△ABC是等腰直角三角形,∠C=90°,AC=BC=2, ∴AB=
∴∠OAB=∠CAB+∠OAC=45°+45°=90°, ∴OB=
(3)如图3, 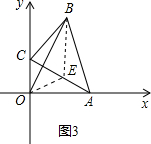 取AC的中点E,连接OE,BE. 在Rt△AOC中,OE是斜边AC上的中线, 所以OE=
在△ACB中,BC=2,CE=
所以BE=
若点O,E,B不在一条直线上,则OB<OE+BE=1+
若点O,E,B在一条直线上,则OB=OE+BE=1+
所以当O,E,B三点在一条直线上时,OB取得最大值,最大值为1+
|
题目简介
如图,在平面直角坐标系中,已知等腰直角三角形ABC,∠C=90°,AC=BC=2,点A、C分别在x轴、y轴上,当点A从原点开始在x轴的正半轴上运动时,点C在y轴正半轴上运动.(1)当A在原点-数学
题目详情
、y轴上,当点A从原点开始在x轴的正半轴上运动时,点C在y轴正半轴上运动.
(1)当A在原点时,求点B的坐标;
(2)当OA=OC时,求原点O到点B的距离OB;
(3)在运动的过程中,求原点O到点B的距离OB的最大值,并说明理由.