(1)沿x轴正方向射出的粒子恰好从O1点的正上方的P点射出,运动轨迹如图所示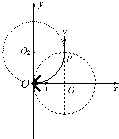 由几何关系可得R=a ① 设圆形磁场区域内的磁感应强度为B,带电粒子在磁场中所受的洛伦兹力提供向心力:qvB=m
①②联立得;B=
由左手定则判断磁场方向垂直于xOy平面向里 (2)经分析,沿与x轴45°向下射出的带电粒子在磁场中运动的时间最长,轨迹如图, 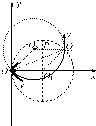 根据几何关系粒子离开磁场时速度方向沿y轴正方向,∠OO3Q=135°. 设该带电粒子在磁场中运动的时间为t,根据圆周运动周期公式得:T=
所以tmax=
①③④联立得:tmax=
(3)设某带电粒子从放射源射出,速度方向与x轴的夹角为α,做速度v的垂线,截取OO4=a,以O4为圆心a为半径做圆交磁场边界于M点.如图所示: 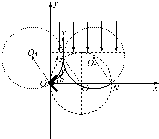 由于圆形磁场的半径与带电粒子在磁场中运动的半径均为a,故OO1MO4构成一个菱形,所以O4M与x轴平行,因此从放射源中射出的所有带电粒子均沿y轴正方向射出.带电粒子在匀强电场中做匀减速直线运动,返回磁场时的速度与离开磁场时的速度大小相等方向相反,再进入磁场做圆周运动,圆心为O5,OO4O5N构成一平行四边形,所以粒子在磁场中两次转过的圆心角之和为180°,第二次离开磁场时都经过N点.故收集器应放在N点,N点坐标为(2a,0). 答:(1)圆形区域内磁感应强度的大小为B=
(2)a、最长时间tmax=
b、(2a,0). |
题目简介
如图所示,在坐标系xOy所在平面内有一半径为a的圆形区域,圆心坐标O1(a,0),圆内分布有垂直xOy平面的匀强磁场.在坐标原点O处有一个放射源,放射源开口的张角为90°,x轴为它-物理
题目详情
(1)求圆形区域内磁感应强度的大小和方向;
(2)a.判断沿什么方向射入磁场的带电粒子运动的时间最长,并求最长时间;
b.若在y≥a的区域内加一沿y轴负方向的匀强电场,放射源射出的所有带电粒子运动过程中将在某一点会聚,若在该点放一回收器可将放射源射出的带电粒子全部收回,分析并说明回收器所放的位置.