| (1)PQ∥MN. ∵四边形ABCD是矩形,∴AD∥BC,且M在AD直线上,则有AM∥BC. ∴∠AMP=∠MPC. 由翻折可得:∠MPQ=∠CPQ=
∠NMP=∠AMN=
∴∠MPQ=∠NMP,故PQ∥MN. 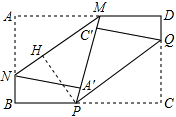 (2)两折痕PQ,MN间的距离不变. 过P作PH⊥MN,则PH=PM?sin∠PMH, ∵∠QPC的角度不变, ∴∠C'PC的角度也不变,则所有的PM都是平行的. 又∵AD∥BC, ∴所有的PM都是相等的. 又∵∠PMH=∠QPC,故PH的长不变. (3)当∠QPC=45°时, 四边形PCQC'是正方形, 四边形C'QDM是矩形. ∵C'Q=CQ,C'Q+QD=a, ∴矩形C'QDM的周长为2a. 同理可得矩形BPA'N的周长为2a,∴两个四边形的周长都为2a,与b无关. |
题目简介
如图1,矩形纸片ABCD的边长分别为a,b(a<b).将纸片任意翻折(如图2),折痕为PQ.(P在BC上),使顶点C落在四边形APCD内一点C′,PC′的延长线交直线AD于M,再将纸片的另一部分翻折-
题目详情
(1)猜想两折痕PQ,MN之间的位置关系,并加以证明;
(2)若∠QPC的角度在每次翻折的过程中保持不变,则每次翻折后,两折痕PQ,MN间的距离有何变化?请说明理由;
(3)若∠QPC的角度在每次翻折的过程中都为45°(如图4),每次翻折后,非重叠部分的四边形MC′QD,及四边形BPA′N的周长与a,b有何关系,为什么?