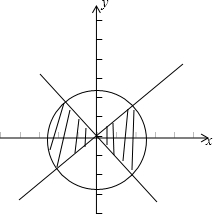
 ∵集合A={(x,y)|x2+y2≤1}, 集合B={(x,y)|log|x||y|≤log|y||x|,|x|<1,|y|<1}={(x,y)||x|<|y|},, 在平面中作出A和B的图象, 结合图象,知A∩B所表示的平面区域的面积为圆x2+y2=1的面积的一半,即
故选D. |
 ∵集合A={(x,y)|x2+y2≤1}, 集合B={(x,y)|log|x||y|≤log|y||x|,|x|<1,|y|<1}={(x,y)||x|<|y|},, 在平面中作出A和B的图象, 结合图象,知A∩B所表示的平面区域的面积为圆x2+y2=1的面积的一半,即
故选D. |
题目简介
设集合A={(x,y)|x2+y2≤1},集合B={(x,y)|log|x||y|≤log|y||x|,|x|<1,|y|<1},则在直角坐标平面内,A∩B所表示的平面区域的面积为()A.πB.34π
题目详情