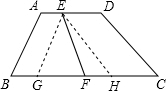
 过点E作EG∥AB交BC于点G,作EH∥CD交BC于点H, 又∵AD∥BC, ∴四边形ABGE,四边形EHCD都是平行四边形, ∴AE=BG=ED=CH,AB=EG,CD=EH,且∠EGH=∠B,∠EHG=∠C, ∴EF是△EGH的中线, ∵∠B+∠C=90°, ∴∠EGH+∠EHG=90°, ∴△EGH是直角三角形, ∵AB=6,CD=8, ∴GH=
∴EF=
故选A. |
 过点E作EG∥AB交BC于点G,作EH∥CD交BC于点H, 又∵AD∥BC, ∴四边形ABGE,四边形EHCD都是平行四边形, ∴AE=BG=ED=CH,AB=EG,CD=EH,且∠EGH=∠B,∠EHG=∠C, ∴EF是△EGH的中线, ∵∠B+∠C=90°, ∴∠EGH+∠EHG=90°, ∴△EGH是直角三角形, ∵AB=6,CD=8, ∴GH=
∴EF=
故选A. |
题目简介
如图,在梯形△ABCD中,AD∥BC,E,F分别是AD,BC的中点,若∠B+∠C=90°,AB=6,CD=8,则EF的长是()A.5B.6C.8D.10-数学
题目详情