| 方法一:如图1,延长ED至M,使MD=ED,连接CM,FM, ∵D为BC中点, ∴BD=CD, 在△BDE和△CDM中, ∵
∴△BDE≌△CDM(SAS), ∴CM=BE,∠B=∠MCD=45°, 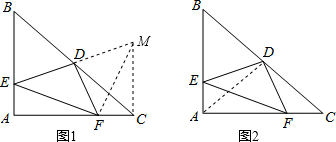 ∴∠MCF=∠MCD+∠ACB=45°+45°=90°, 在Rt△MCF中,MF=
∵DE⊥DF,MD=ED, ∴EF=MF=13; 方法二:如图2,连接AD, ∵△ABC是等腰直角三角形,点D为BC的中点, ∴AD=CD,∠DAE=∠C=45°,AD⊥BC, ∴∠ADF+∠CDF=90°, ∵DE⊥DF, ∴∠ADE+∠ADF=90°, ∴∠ADE=∠CDF, 在△ADE和△CDF中, ∵
∴△ADE≌△CDF(ASA), ∴AE=CF, 同理可得AF=BE, 在Rt△AEF中,EF=
|
题目简介
△ABC中,AB=AC,∠BAC=90°,D为BC中点,DE⊥DF,若BE=12,CF=5,求EF的长.-数学
题目详情