 (1)证明:∵△ABC是等腰直角三角形,∠C=90°, ∴∠B=∠A=45°, ∵四边形DEFG是正方形, ∴∠BFG=∠AED=90°, 故可得出∠BGF=∠ADE=45°,GF=ED, ∵在△ADE与△BGF中,
∴△ADE≌△BGF(ASA); (2)过点C作CG⊥AB于点G, ∵正方形DEFG的面积为16cm2, ∴DE=AE=4cm, ∴AB=3DE=12cm, ∵△ABC是等腰直角三角形,CG⊥AB, ∴AG=
在Rt△ADE中, ∵DE=AE=4cm, ∴AD=
∵CG⊥AB,DE⊥AB, ∴CG∥DE, ∴△ADE∽△ACG, ∴
解得AC=6
|
题目简介
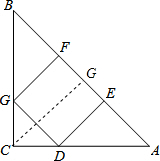
如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D地边AC上,点E、F在边AB上,点G在边BC上.(1)求证:△ADE≌△BGF;(2)若正方形DEFG的面积为16cm2,求AC的长.-
题目详情
(1)求证:△ADE≌△BGF;
(2)若正方形DEFG的面积为16cm2,求AC的长.