 (1)证明:∵△ACB和△ECD都是等腰直角三角形, ∴AC=BC,CE=CD,∠ACE=∠BCD=90°, 在△ACE和△BCD,
∴△ACE≌△BCD(SAS); (2)直线AE与BD互相垂直,理由为: 证明:∵△ACE≌△BCD, ∴∠EAC=∠DBC, 又∵∠DBC+∠CDB=90°, ∴∠EAC+∠CDB=90°, ∴∠AFD=90°, ∴AF⊥BD, 即直线AE与BD互相垂直. |
 (1)证明:∵△ACB和△ECD都是等腰直角三角形, ∴AC=BC,CE=CD,∠ACE=∠BCD=90°, 在△ACE和△BCD,
∴△ACE≌△BCD(SAS); (2)直线AE与BD互相垂直,理由为: 证明:∵△ACE≌△BCD, ∴∠EAC=∠DBC, 又∵∠DBC+∠CDB=90°, ∴∠EAC+∠CDB=90°, ∴∠AFD=90°, ∴AF⊥BD, 即直线AE与BD互相垂直. |
题目简介
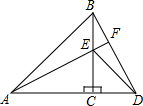
如图,△ACB和△ECD都是等腰直角三角形,A,C,D三点在同一直线上,连接BD,AE,并延长AE交BD于F.(1)求证:△ACE≌△BCD;(2)直线AE与BD互相垂直吗?请证明你的结论.-数学
题目详情
E交BD于F.
(1)求证:△ACE≌△BCD;
(2)直线AE与BD互相垂直吗?请证明你的结论.