(1)证明:∵CD⊥AD,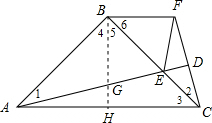 ∴∠ADC=90°, ∴AD2+CD2=AC2, 而AD2+CD2=2AB2, ∴AC2=2AB2, ∵∠ABC=90°, ∴AB2+BC2=AC2, ∴2AB2=AB2+BC2, ∴AB=BC; (2)证明:过B点作BH⊥AC于H,交AE于G点,如图, ∵AB=AC,∠ABC=90°, ∴△ABC为等腰直角三角形, ∴∠3=∠4=∠5=45°, ∵∠AGH+∠GAH=90°,∠2+∠3+∠CAD=90°, ∴∠AGH=∠2+∠3, 而∠AGH=∠1+∠4, ∴∠1=∠2; ∵BF∥AC, ∴∠6=∠3=45°, ∴∠4=∠6, ∵在△ABG和△CBF中,
∴△ABG≌△CBF(ASA), ∴AG=CF,BG=BF, ∵在△BGE和△BFE中,
∴△BGE≌△BFE(SAS), ∴GE=EF, 而AE=AG+GE, ∴AE=CF+EF. |
题目简介
已知如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2(1)求证:AB=BC;(2)过B作BF∥AC交CD的延长线于F,连EF,求证:AE=CF+EF.-数学
题目详情
(1)求证:AB=BC;
(2)过B作BF∥AC交CD的延长线于F,连EF,求证:AE=CF+EF.