如图1，在边长为5的正方形ABCD中，点E、F分别是BC、DC边上的点，且AE⊥EF，BE=2．（1）求EC：CF的值；（2）延长EF交正方形外角平分线CP于点P（如图2），试判断AE与EP的大小关系

题目简介

题目详情

如图1，在边长为5的正方形ABCD中，点E、F分别是BC、DC边上的点，且AE⊥EF，BE=2．
（1）求EC：CF的值；
（2）延长EF交正方形外角平分线CP于点P（如图2），试判断AE与EP的大小关系，并说明理由；
（3）在图2的AB边上是否存在一点M，使得四边形DMEP是平行四边形？若存在，请给予证明；若不存在，请说明理由． 360优课网

题型：解答题难度：中档来源：黔南州

答案

（1）如图1．∵AE⊥EF，
∴∠2+∠3=90°，
∵四边形ABCD为正方形，
∴∠B=∠C=90°，
∵∠1+∠3=90°，
∴∠1=∠2，
∴△ABE∽△ECF，
∴AB：CE=BE：CF，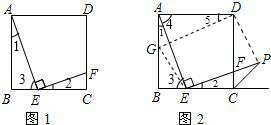
360优课网

∴EC：CF=AB：BE=5：2

（2）如图2，在AB上取BG=BE，连接EG，
∵ABCD为正方形，
∴AB=BC，
∵BE=BG，
∴AG=EC，
在△AGE和△ECP中

∠1=∠2

AG=EC

∠AGE=∠ECP

，
∴△AGE≌△ECP（ASA），
∴AE=EP；

（3）存在．顺次连接DMEP．
如图2．
在AB取点M，使AM=BE，
∵AE⊥EF，
∴∠2+∠3=90°，
∵四边形ABCD为正方形，
∴∠B=∠BCD=90°，
∴∠1+∠3=90°，
∴∠1=∠2，
∵∠DAM=∠ABE=90°，DA=AB，

AD=AB

∠DAM=∠ABE

AM=BE

∴△DAM≌△ABE（SAS），
∴DM=AE，
∵AE=EP，
∴DM=PE，
∵∠1=∠5，∠1+∠4=90°，
∴∠4+∠5=90°，
∴DM⊥AE，
∴DM∥PE
∴四边形DMEP是平行四边形．

上一篇 : 已知：∠a=36°，则∠a的余角等于（）
下一篇 : 如图，△ABC的高AD、BE相交于点O

如图1，在边长为5的正方形ABCD中，点E、F分别是BC、DC边上的点，且AE⊥EF，BE=2．（1）求EC：CF的值；（2）延长EF交正方形外角平分线CP于点P（如图2），试判断AE与EP的大小关系

题目简介

题目详情

答案

更多内容推荐