 证明:(1)如图,连接AP并延长, ∵PE⊥AB,PF⊥AC ∴∠AEP=∠AFP=90° 又AE=AF,AP=AP, ∵在Rt△AFP和Rt△AEP中
∴Rt△AEP≌Rt△AFP(HL), ∴PE=PF. (2)∵Rt△AEP≌Rt△AFP, ∴∠EAP=∠FAP, ∴AP是∠BAC的角平分线, 故点P在∠BAC的角平分线上. |
 证明:(1)如图,连接AP并延长, ∵PE⊥AB,PF⊥AC ∴∠AEP=∠AFP=90° 又AE=AF,AP=AP, ∵在Rt△AFP和Rt△AEP中
∴Rt△AEP≌Rt△AFP(HL), ∴PE=PF. (2)∵Rt△AEP≌Rt△AFP, ∴∠EAP=∠FAP, ∴AP是∠BAC的角平分线, 故点P在∠BAC的角平分线上. |
题目简介
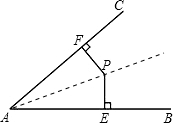
如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.求证:(1)PE=PF;(2)点P在∠BAC的角平分线上.-数学
题目详情
求证:
(1)PE=PF;
(2)点P在∠BAC的角平分线上.