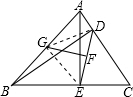
 GF⊥DE.理由如下: 如图,连接GE、GD. ∵AE,BD分别是三角形ABC的BC,AC边上的高, ∴∠AEB=90°,∠ADB=90°, ∴在Rt△ABE中,G是斜边AB的中点,则GE=
同理,GD=
∴GD=GE. 又∵F是DE的中点, ∴GF⊥DE. |
 GF⊥DE.理由如下: 如图,连接GE、GD. ∵AE,BD分别是三角形ABC的BC,AC边上的高, ∴∠AEB=90°,∠ADB=90°, ∴在Rt△ABE中,G是斜边AB的中点,则GE=
同理,GD=
∴GD=GE. 又∵F是DE的中点, ∴GF⊥DE. |
题目简介
如图,已知AE,BD分别是三角形ABC的BC,AC边上的高,F是DE的中点,G是AB的中点,试说明GF与DE的位置关系.-数学
题目详情