如图所示，在以O为圆心，半径为R的圆形区域内，有一个水平方向的匀强磁场，磁场的磁感应强度大小为B，方向垂直纸面向外．竖直平行正对放置的两金属板A、K连在电压可调的电路中-物理

题目简介

题目详情

如图所示，在以O为圆心，半径为R的圆形区域内，有一个水平方向的匀强磁场，磁场的磁感应强度大小为B，方向垂直纸面向外．竖直平行正对放置的两金属板A、K连在电压可调的电路中． S₁、S₂为A、K板上的两个小孔，且S₁、S₂和O在同一直线上，另有一水平放置的足够大的荧光屏D，O点到荧光屏的距离h．比荷（电荷量与质量之比）为k的带正电的粒子由S₁进入电场后，通过S₂射向磁场中心，通过磁场后落到荧光屏D上．粒子进入电场的初速度及其所受重力均可忽略不计．
（1）求粒子垂直打到荧光屏上M点时速度的大小；
（2）调节滑片P，使粒子打在荧光屏上N点，MN=

/3h（如图所示），求此时A、K两极板间的电压． 360优课网

题型：问答题难度：中档来源：不详

答案

（1）设粒子的质量为m，电荷量为q，垂直打在荧光屏上的M点时的速度为v1，粒子垂直打在荧光屏上，说明粒子在磁场中的运动是四分之一圆周，
运动半径：r1=R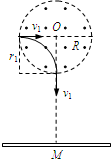

360优课网

根据牛顿第二定律：Bqv1=m

依题意：k=class="stub"q

解得：v1=BkR
（2）设粒子在磁场中运动轨道半径为r2，偏转角为2θ，粒子射出磁场时的方向与竖直方向夹角为α，粒子打到N点时的轨迹如图所示，由几何关系可知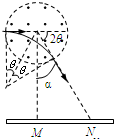

360优课网

tanα=class="stub"MN

，α=30°，θ=30°
tanθ=class="stub"R

解得：r2=

R
设此时A、K两极板间的电压为U，设粒子离开S2时的速度为v2，
根据牛顿第二定律：Bqv2=m

根据动能定理有 qU=class="stub"1

解得：U=class="stub"3

kB2R2
答：（1）粒子垂直打到荧光屏上M点时速度的大小为BkR；
（2）此时A、K两极板间的电压为U=class="stub"3

kB2R2．

上一篇 : 如图所示，一个圆盘圆心为O，水平
下一篇 : 如图所示，在匀速转动的水平转盘

如图所示，在以O为圆心，半径为R的圆形区域内，有一个水平方向的匀强磁场，磁场的磁感应强度大小为B，方向垂直纸面向外．竖直平行正对放置的两金属板A、K连在电压可调的电路中-物理

题目简介

题目详情

答案

更多内容推荐