| 设甲种设备需要生产x天,乙种设备需要生产y天,该公司所需租赁费为z元,则z=200x+300y,(2分) 甲、乙两种设备生产A,B两类产品的情况为下表所示:
则满足的关系为
作出不等式表示的平面区域, 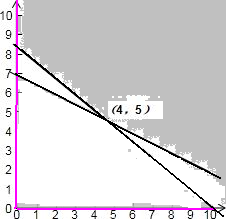 当z=200x+300y对应的直线过两直线
目标函数z=200x+300y取得最低为2300元.(12分) |
| 设甲种设备需要生产x天,乙种设备需要生产y天,该公司所需租赁费为z元,则z=200x+300y,(2分) 甲、乙两种设备生产A,B两类产品的情况为下表所示:
则满足的关系为
作出不等式表示的平面区域,  当z=200x+300y对应的直线过两直线
目标函数z=200x+300y取得最低为2300元.(12分) |
题目简介
某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备-数学
题目详情