连CF,如图,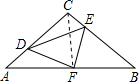 ∵F点是等腰Rt△ABC边AB中点, ∴CF=FA,CF⊥AB,CF平分∠ACB, ∴∠FCE=∠A=45°,∠CFA=90°, 又∵∠DFE=90°, ∴∠AFD=∠CFE, 在△AFD和△CFE中
∴△AFD≌△CFE, ∴FD=FE, ∴△DFE是等腰直角三角形; ∵四边形CDFE的面积=△CDF的面积+△CFE的面积=△CDF的面积+△AFD的面积=△CAF的面积=
当FD⊥AC时,四边形CDFE为正方形,此时△CDE面积的最大值为
故选D. |
连CF,如图, ∵F点是等腰Rt△ABC边AB中点, ∴CF=FA,CF⊥AB,CF平分∠ACB, ∴∠FCE=∠A=45°,∠CFA=90°, 又∵∠DFE=90°, ∴∠AFD=∠CFE, 在△AFD和△CFE中
∴△AFD≌△CFE, ∴FD=FE, ∴△DFE是等腰直角三角形; ∵四边形CDFE的面积=△CDF的面积+△CFE的面积=△CDF的面积+△AFD的面积=△CAF的面积=
当FD⊥AC时,四边形CDFE为正方形,此时△CDE面积的最大值为
故选D. |
题目简介
如图,在等腰Rt△ABC中,∠C=90°,AC=8,将直角尺的顶点放在边AB中点F上,直角尺的两边分别交AC、BC于点D、E,连接DE,直角尺在旋转的过程中,下列结论不正确的是()A.△DFE是等-数
题目详情