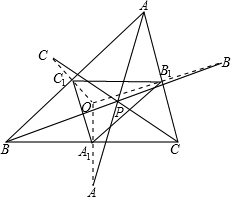
 证明:(1)设圆O半径为R. 由△ABC的外心O关于三边的对称点分别为A′、B′、C′, 知:BC′=B′C=R,∠C′BA=∠C′AB=∠OAB,∠B′CA=∠B′AC=∠OAC, ∴∠C′BA+∠B′CA=∠OAB+∠OAC=∠BAC, ∴∠C′BC+∠B′CB=∠BAC+∠ABC+∠BCA=180°, ∴BC′∥B′C, ∴BB′,CC′互相平分,交于中点, 同理CC′,AA′互相平分,交于中点, ∴AA′、BB′、CC′交于一点P; (2)∵P为CC′中点,A1为BC中点, ∴PA1=
同理PB1=
∴PA1=PB1=PC1, ∴P是△A1B1C1的外心. |
题目简介
如图,△ABC的外心O关于三边的对称点分别为A′、B′、C′.求证:(1)AA′、BB′、CC′交于一点P;(2)设△ABC三边中点分别为A1、B1、C1,则P为△A1B1C1的外心.-数学
题目详情
(1)AA′、BB′、CC′交于一点P;
(2)设△ABC三边中点分别为A1、B1、C1,则P为△A1B1C1的外心.