如图所示，两个轻质小环A、B套在光滑固定的水平杆上，两环间距为a，用原长为L的轻质橡皮条分别连接两环（a＜l＜2a），在橡皮条中间加一竖直向上的力F，在两环上分别施加大小相等-物理

题目简介

如图所示，两个轻质小环A、B套在光滑固定的水平杆上，两环间距为a，用原长为L的轻质橡皮条分别连接两环（a＜l＜2a），在橡皮条中间加一竖直向上的力F，在两环上分别施加大小相等的作用力，使橡皮条拉成一个与杆围成边长为a的正三角形保持平衡，则关于施加在两环上的作用力，下列说法中正确的是（　　）

A．若沿橡皮条方向，大小应为

B．若沿垂直橡皮条方向，大小应为

C．若沿杆方向，大小应为

D．最小值为

题型：多选题难度：偏易来源：不详

A、将拉力F沿着两根橡皮条方向进行分解，如图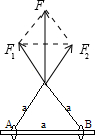

360优课网

根据平行四边形定则，得到两个分力为：2F1cos30°=F，解得，F1=F2=

F；
若沿橡皮条方向施加力时，外力必须与F1和F2平衡时，即大小等于

F，环保持静止，故A正确；
B、若沿垂直橡皮条方向施加力T，橡皮条受到的拉力和另外施加的力合力向上，如图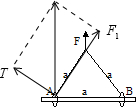

360优课网

由几何关系得到，T=

F1=class="stub"1

F，故B正确；
C、C、若沿杆方向施加力T，橡皮条橡皮条受到的拉力和另外施加的力合力依然向上，如图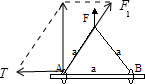

360优课网

由几何关系得到，T=class="stub"1

F1=

F，故C错误；
D、不管沿着什么方向施加力T，该与橡皮条的拉力的合力一定沿着竖直方向，通过作图可知，当施加力方向与合力方向垂直时，该力最小，由C选项结论可知最小力为

F，故D正确；
故选ABD．