| (1)如图2,AH=1+1+1=3,CH=1, 即最长线段AC的长度是:
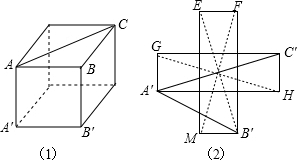 (2)连接B′C′, 由图形可知:∠A′B′E=∠C′B′E=45°,A′B′=B′C′=
∴∠A′B′C′=90°, 即△A′B′C′是等腰直角三角形, ∴∠B′A′C′=45°; 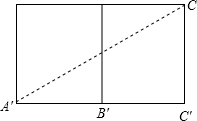 (3)如图所示展开:连接A′C,则线段A′C的长就是蚂蚁从点A′沿着正方体的表面爬行到点C的最短路程, 在Rt△A′C′C中,A′C′=1+1=2,C′C=1,∠A′C′C=90°, 由勾股定理得:A′C=
|
| (1)如图2,AH=1+1+1=3,CH=1, 即最长线段AC的长度是:
 (2)连接B′C′, 由图形可知:∠A′B′E=∠C′B′E=45°,A′B′=B′C′=
∴∠A′B′C′=90°, 即△A′B′C′是等腰直角三角形, ∴∠B′A′C′=45°;  (3)如图所示展开:连接A′C,则线段A′C的长就是蚂蚁从点A′沿着正方体的表面爬行到点C的最短路程, 在Rt△A′C′C中,A′C′=1+1=2,C′C=1,∠A′C′C=90°, 由勾股定理得:A′C=
|
题目简介
如果(1)所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图(2)所示已知展开图中每个正方形的边长为1.(1)求在该展开图中可画出的最长线段的长度?这样的线段可以画几条-数学
题目详情
图,如图(2)所示已知展开图中每个正方形的边长为1.
(1)求在该展开图中可画出的最长线段的长度?这样的线段可以画几条?
(2)求∠B′A′C′的度数?说明理由.
(3)在图1中若蚂蚁从点A′沿着正方体的表面爬行到点C,试求爬行的最短路程.