 (1)设质子在磁场I和II中做圆周运动的轨道半径分别为r1和r2,区域II中磁感应强度为B′, 由牛顿第二定律qvB=m
qvB/=m
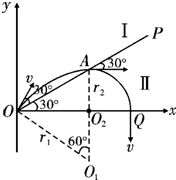
粒子在两区域运动的轨迹如图所示,由几何关系可知,质子从A点出磁场I时的速度方向与OP的夹角为300,故质子在磁场I中轨迹的圆心角为 θ=60° 则△O1OA为等边三角形 OA=r1 ③r2=OAsin30°④ 由①②③④解得区域II中磁感应强度为 B′=2B (2)Q点坐标 x=OAcos30°+r2=r1cos30°+r2 故 x=(
答:(1)区域II中磁场的磁感应强度大小为2B; (2)Q点的坐标x=(
|
题目简介
如图所示,在空间有一坐标系xoy,直线OP与x轴正方向的夹角为30°,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP是他们的边界,OP上方区域I中磁场的磁感应-物理
题目详情
(1)区域II中磁场的磁感应强度大小;
(2)Q点的坐标.