如图所示为圆形区域的匀强磁场，磁感应强度为B、方向垂直纸面向里，边界跟y轴相切于坐标原点O．O点处有一放射源，沿纸面向各方向射出速率均为v的某种带电粒子，带电粒子在磁场-物理

题目简介

题目详情

如图所示为圆形区域的匀强磁场，磁感应强度为B、方向垂直纸面向里，边界跟y轴相切于坐标原点O． O点处有一放射源，沿纸面向各方向射出速率均为v的某种带电粒子，带电粒子在磁场中做圆周运动的半径是圆形磁场区域半径的两倍．已知该带电粒子的质量为m、电荷量为q，不考虑带电粒子的重力．
（1）推导带电粒子在磁场空间做圆周运动的轨道半径；
（2）求带电粒子通过磁场空间的最大偏转角；
（3）沿磁场边界放置绝缘弹性挡板，使粒子与挡板碰撞后以原速率弹回，且其电荷量保持不变．若从O点沿x轴正方向射入磁场的粒子速度已减小为

，求该粒子第一次回到O点经历的时间． 360优课网

题型：问答题难度：中档来源：不详

答案

（1）带电粒子进入磁场后，受洛伦兹力作用，由牛顿第二定律得：
Bqυ=m

υ2

r=class="stub"mυ

（2）设粒子飞出和进入磁场的速度方向夹角为?，则sinclass="stub"φ

=class="stub"x

，x是粒子在磁场中轨迹的两端点的直线距离．
x最大值为2R，对应的就是φ最大值．且2R=r
所以sin

φmax

=class="stub"R

=class="stub"1

，φmax=60°．
（3）当粒子的速度减小为class="stub"v

时，在磁场中作匀速圆周运动的半径为r1=class="stub"mv

2qB

=R
故粒子转过四分之一圆周，对应圆心角为90°时与边界相撞弹回，由对称性知粒子经过四个这样的过程后第一次回到O点，亦即经历时间为一个周期．
粒子在磁场中做匀速圆周运动的周期：T=class="stub"2πm

．
所以从O点沿x轴正方向射出的粒子第一次回到O点经历的时间是：t=class="stub"2πm

．
答：（1）带电粒子在磁场空间做圆周运动的轨道半径为class="stub"mυ

；
（2）带电粒子通过磁场空间的最大偏转角为60°；
（3）沿磁场边界放置绝缘弹性挡板，使粒子与挡板碰撞后以原速率弹回，且其电荷量保持不变．若从O点沿x轴正方向射入磁场的粒子速度已减小为class="stub"v

，该粒子第一次回到O点经历的时间为class="stub"2πm

．

上一篇 : 关于电场力与洛伦兹力，以下说法
下一篇 : 如图所示，地球由西向东转．赤道上

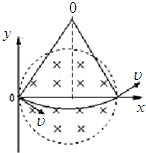
如图所示为圆形区域的匀强磁场，磁感应强度为B、方向垂直纸面向里，边界跟y轴相切于坐标原点O．O点处有一放射源，沿纸面向各方向射出速率均为v的某种带电粒子，带电粒子在磁场-物理

题目简介

题目详情

答案

更多内容推荐